栈-C
栈(Stack)是一种限制插入和删除只能在一个位置上进行操作的表
将他抽象出来类似一个罐子,并且每次存储东西只能将新的物品堆在前一个物品之上,所以这个罐子的出口和入口是同一个,也就意味着每次操作都必须从最顶上的物品开始,最顶上的那个物品我们把它叫做栈顶
如果玩射击游戏的话可以把他理解为是一个弹夹 🔫
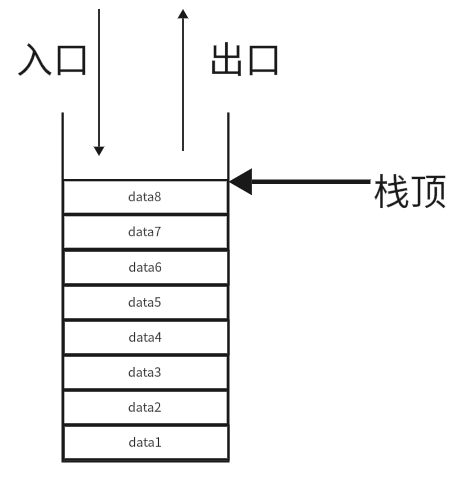
但是这只是他在逻辑上的形式,如果将他存储在内存中还是要使用表的形式
如果将抽象的栈转换成表的形式就会如下所示
栈顶的位置:
- 数组栈就是在数组的末尾
- 链表栈就是在链表的第一个节点(有头节点就是第二个)
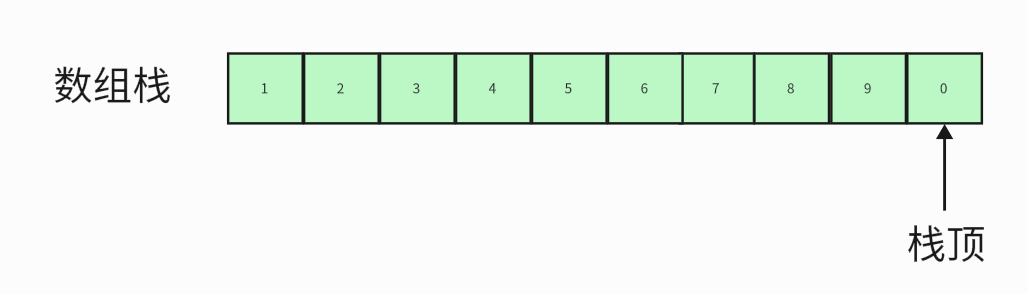
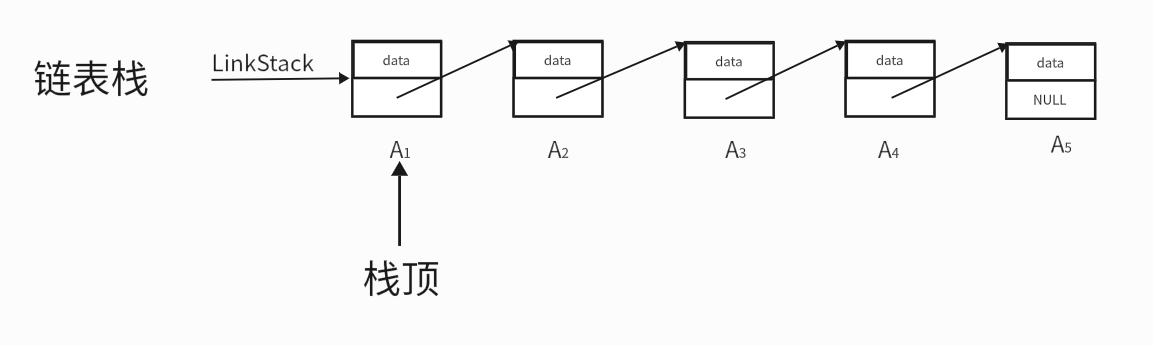
栈的操作
对栈的基本操作一般只有Push(进栈)和Pop(出栈)
- 进栈:就相当于是插入
- 出栈:就相当于是删除最后插入的节点
数组栈
数据栈的结构体
1 | |
elem[Stack_Size]:用来存储栈元素的数组
top:表示栈顶元素的下标
初始化
数组栈的初始化就是给结构体实例化,并且将stack这个指针指向了这个实例化的结构体,并且将栈顶设置为-1表示目前还只是一个空栈
1 | |

进栈
1 | |
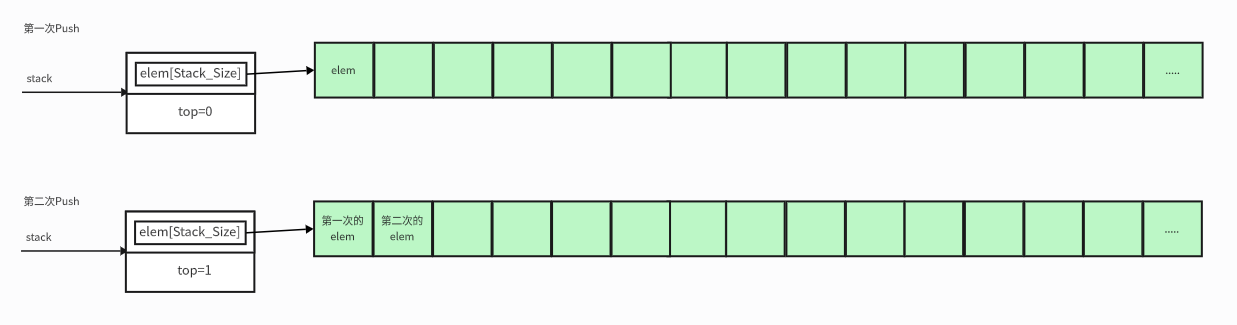
进栈的逻辑如下所示:
- 栈顶对应的下标
+1 - 将
elem赋值给当前栈顶所对应的下标的位置
出栈
1 | |
EmptyStack(*stack)用来判断是不是空栈,只需要判断top是否等于-1即可
出栈的逻辑如下所示:
- 将
top的数据赋值给*elem - 栈顶对应的下标
-1,相当于将原来栈顶给隐藏掉了,将原栈顶的前一个作为新的栈顶
红色为出栈前
蓝色为出栈后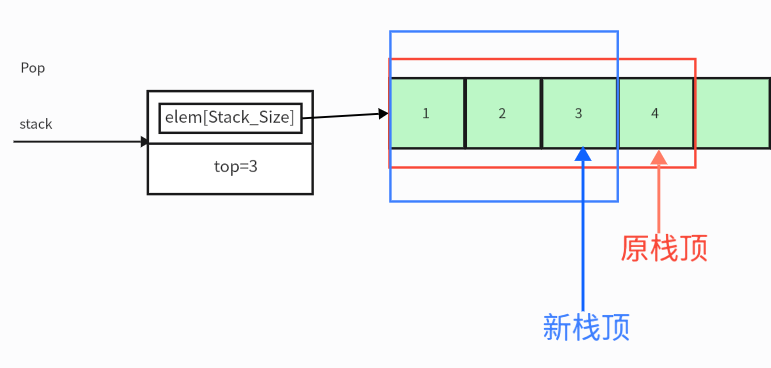
链表栈
链表栈的结构体
1 | |
初始化
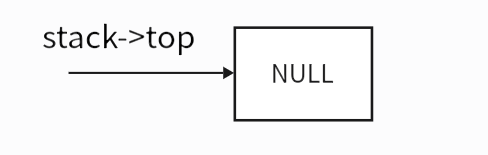
链表栈的初始化就是给结构体实例化,并且将stack->top这个指针指向了这个实例化的结构体,并且将栈顶设置为NULL表示目前还只是一个空栈
1 | |
进栈
1 | |
进栈的逻辑如下所示:
- 实例化一个新节点
node,并把数据赋值给node->data - 将
node->next指向top指向的节点 - 最后把
stack->top指向node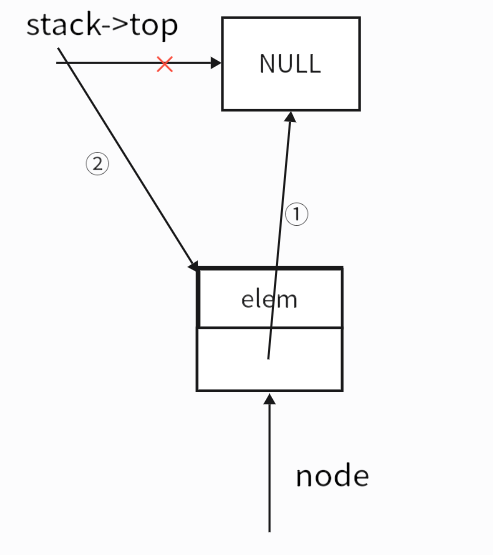
最后呈现的结果如下图所示
出栈
1 | |
EmptyStack(*stack)同样也是一个判断栈是否为空的函数,直接判断stack->top是否等于NULL即可
出栈的逻辑如下所示:
- 创建一个指针
free_node,把他指向top节点,也就是栈顶 - 将栈顶指向
free_node的下一个节点,栈顶下面的第一个节点,作为新的栈顶 - 释放
free_node
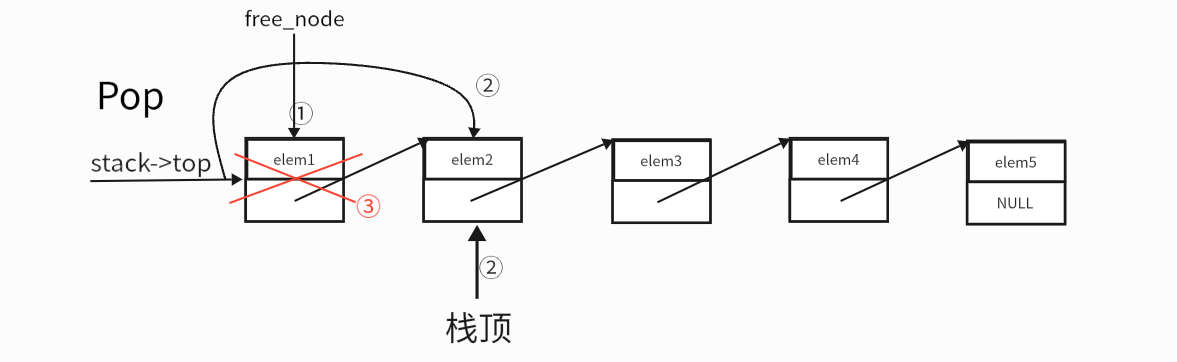
最后呈现的结果如下图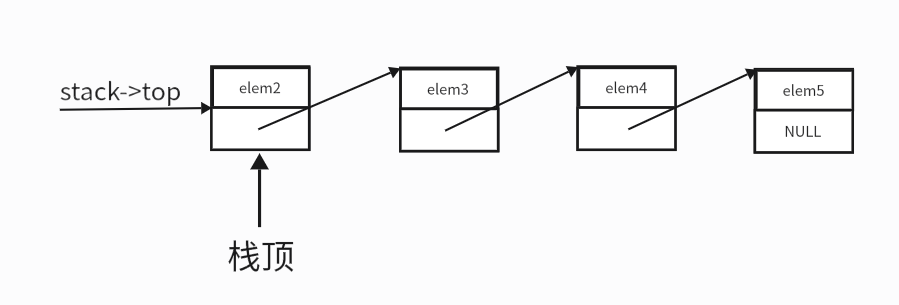
栈-C
http://www.ming-ice-tea.top/2025/10/26/栈-C/